De la ecuación de la pizza al problema del volumen del helado de Coppelia

Encontrarme este video en internet me ha traído muchos recuerdos de la universidad.

No porque comiera muchas pizzas en aquella época, la verdad. Sino del ambiente, de las tonterías y ‘chistes de físicos’ con que nos entreteníamos en aquella Facultad de Física-Matemática de la Universidad de La Habana que nos iba formando profesionalmente, pero que también, poco a poco y sin apenas notarlo, nos iba conformando como personas.

Nosotros también tuvimos nuestro problema de la pizza, pero con bolas de helados: el ‘famoso’ problema del volumen real de los helados de Coppelia…

Lo cuento. Era principios de los años 80 del pasado siglo, y todos los días, al terminar nuestra jornada en la UH, un grupo de gente de primer año nos pasábamos por el Coppelia (la ‘mítica’ heladería habanera que era, y creo que sigue siendo, uno de los centros de la vida social de la ciudad). Se hizo casi una tradición que se mantuvo durante casi toda la carrera. Nos tomábamos un helado, conversábamos un rato, y luego el grupo se rompía y nos íbamos cada uno por nuestro lado.

De la ya escasa oferta de formatos y sabores que se ofertaban en aquella época, nuestros preferidos eran dos: el ‘jimaguas’ y el ‘tres gracias’. El primero tenía dos bolas grandes de helado, y el segundo, tres pequeñas. Y ambos valían lo mismo: un peso. De modo que un día salió la discusión inevitable: ¿cuál era mas rentable? ¿Cuál daba mas helado por el mismo precio?

La respuesta era simple, a primera vista y con unos conocimientos elementales de matemáticas: Como el volumen de una esfera varía con el cubo del radio, el volumen total del jimaguas era mayor que el otro. Hasta ahí, todo bien.

Pero enseguida alguien saltó con una realidad obvia: eso era en esferas ideales, perfectas. En la práctica, en cambio, aquellas bolas de helado que servían en Coppelia eran de todo menos ideales. No había mas que mirarlas. Así que, si tomábamos en consideración todas las imperfecciones reales, ¿se mantendría la regla del volumen y el cubo del radio? ¿Seguía siendo mejor el jimaguas?

El modelo del helado real

Y así surgió el reto: calcular el volumen de las bolas reales. La respuesta seguía siendo casi inmediata, pero ya en la carrera nos empezaban a meter bien en la cabeza que las cosas en ciencia hay que demostrarlas. Además, por aquella época estábamos dando en Análisis Matemático lo de las integrales triples, de modo que de paso practicábamos un poco con algo que no fueran los ya manoseados ejercicios de los libros… Y bueno, ya digo, éramos jóvenes y ya nos hacían gracia esos chistes. Así que un día en la biblioteca alguien sacó un folio y nos pusimos manos a la obra.

Ya no recuerdo bien los detalles, pero sí cómo lo resolvimos: construimos un modelo basado en una esfera ideal intersectada por varios planos, que simularían las imperfecciones de las bolas de helado reales. Pusimos un plano horizontal por abajo, porque las bolas estaban siempre aplastadas en el fondo; luego otro igual por arriba, porque siempre el dependiente le hacía una muesca a la bola de helado con la cuchara al servirla (para quitarle un trozo); pusimos otro vertical, a un lado, porque siempre las bolas, pegadas, se aplastaban entre sí; y finalmente, creo, pusimos otro oblicuo en un lado, porque las bolas también se aplastaban en el borde de la copa.

Quedó algo así:

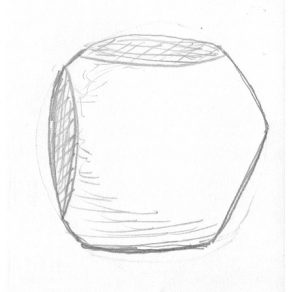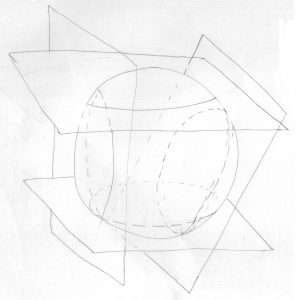
No era exacto, en aquellas bolas había mas historias, pero nos valió. En realidad, recuerdo los jimaguas mas o menos así:

Pero bueno, en un rato calculamos el volumen del cuerpo resultante. Y repito que no recuerdo bien lo que nos quedó, pero sí que la conclusión fue clara: aún para aquellos desastres de bolas de helado el volumen seguía variando casi, razonablemente, según la fórmula del cubo del radio. Es decir, los jimaguas seguían dando mas por el mismo precio.

Una tontería, vale, pero era primer año y fue la primera vez que lo que estaba aprendiendo en la carrera me servía para resolver un problema de mi vida real. Y además echamos unas risas en el grupo de amigos que ya se iba formando…

En fin. Chistes de matemáticos. Recuerdos de una época (¡los años 80 en Cuba, madre mía!) que ya me queda tan lejana…

Y todo por encontrarme por ahí el vídeo de la ecuación de la pizza.